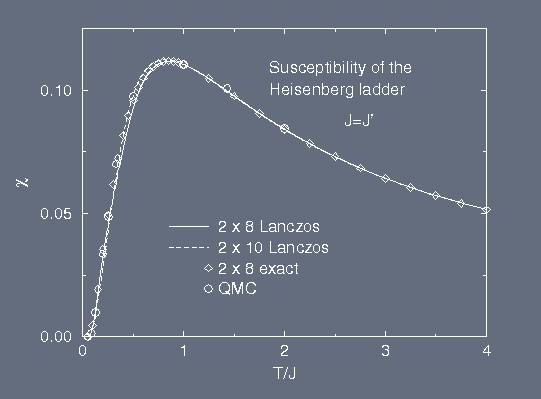Finite-Temperature Lanczos Method
The method is designed for calculation of dynamical and statical correlation
functions in small systems at finite temperatures (see. J. Jaklic and P. Prelovsek,
Phys. Rev. B 49 , 5065-8 (1994)).
It has been applied to variety of models (e.g. t-J, Hubbard,
Heisenberg) and the problems studied so far include:
- optical conductivity
- dynamical spin susceptibility and NMR relaxation
- Raman scattering,
- uniform spin susceptibility
- entropy and specific heat
- spectral functions and photoemission spectra
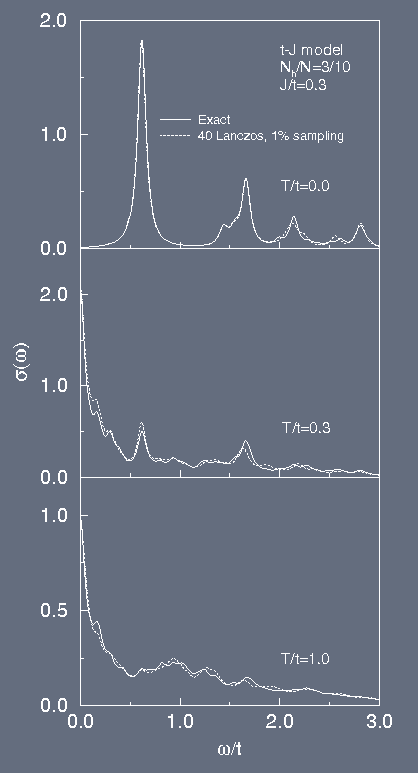
Example 1: optical conductivity of the two-dimensional t-J model
Shown is the optical conductivity for 7 electrons on 10 lattice sites.
- Exact result:
- full diagonalization, matrices up to 420 x 420
- FT Lanczos method:
- 1% random sampling and 40 Lanczos steps
- Largest system treated so far:
- 15 electrons on 18 sites (exact result would require diagonalization of
291720 x 291720 matrix)
Example 2: spin susceptibility of two coupled Heisenberg chains
The figure shows comparison of the results obtained with the Lanczos method
to the results of exact diagonalization and Quantum Monte Carlo.
The 2 x 10 Lanczos results were obtained by sampling over ~1000 random
states and using ~30 Lanczos steps. The calculation took around 1 hour
of CPU on Convex 3800. Exact result would require several full diagonalisations of
matrices with sizes up to 9278 x 9278.
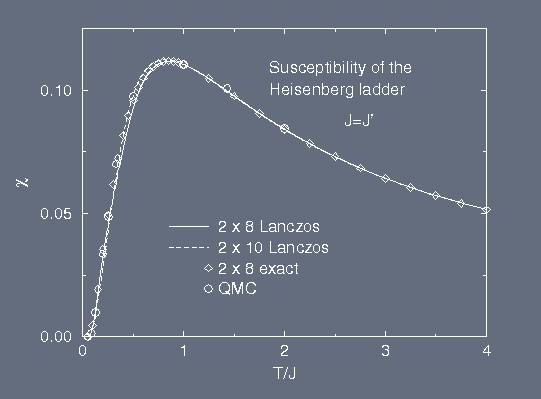
Last update made on June 20, 1996 by J.J.